Archive: Dropout and batch normalization

Working on Dropout & Batchnorm. I decided to do Dropout first, since the Batchnorm papers the course references assume the reader has experience with models which use Dropout. The two can be used in tandem.

Dropout

So, per the course notes & its referenced papers, dropout is a form of regularization to be used in complement with traditional L1/L2 norm regularization. It was created in response to an overfitting problem unique to multi-layer neural nets - deeper networks learn feature detectors which are over-reliant on specific neurons upstream behaving in a very particular manner in train. When test data is fed in, the training conditions which yielded the codependent detectors no longer exists, and predictive capability drops accordingly. We would prefer each layer of a given network be more independent from the layer (or composition of layers) which precedes it.

Before dropout, this was mitigated by training multiple neural nets with different weight initializations on input samples, then taking the average prediction over all trained nets in test.

With vanilla dropout, a similar effect is achieved within a single network’s training phase by randomly keeping a fixed percentage $p$ of neurons after each activation function, randomly selecting $(1-p)$ neurons and setting them to 0. In test, you stop dropping neurons, and scale predictions by $1/p$. The result is analogous to taking the average prediction of multiple nets, but only requires training a single network.

In the coursework, they have you implement inverted dropout, then use it on the fully-connected net, which I’ve done.

Batch Normalization:

Batch normalization is a straightforward procedure to describe - during training, after the affine transform is applied at each layer, you calculate the mean and standard deviation $(\mu, \sigma)$ of each feature in the output batch, then use those values to normalize the batch such that the data are centered at 0 with standard deviation of 1. This should feel familiar, since you’re generally doing this as a preprocessing step on raw data before inputting it to your model’s first layer - except now it’s being used between each layer. Another difference is that we choose some $\beta$ and $\lambda$ to adjust the center and spread of the batch, respectively. Finally, the current layer’s $\mu, \sigma$ are added to the overall running average and stddev (which are each scaled by a momentum factor). The running stats are used in Test instead of layer-specific ones - and then transformed by the same $\beta, \lambda$.

By re-distributing about the $\beta, \lambda$ we choose, we can speculate why the relative frequency of Dropout can be considerably reduced (or tossed altogether) when combined with batch normalization. It’s possibly because we already have control of the relative frequency of dropped activations - for example, setting $\beta=0$ leaves the data zero-centered, so we expect 50% of the scores to be negative and get dropped by the activation function. This also ensures we stay away from the saturation points (outer edges) of the activation function which helps mitigate the likelihood of exploding/vanishing gradients.

Benefits: As mentioned, we’ve reduced the occurrence of unstable gradients. From this, it follows that our models can tolerate a wider range of hyperparameter settings such as higher learning rates, or different weight initialization schemes. As per Ioffe & Szegedy’s original findings, model accuracy tends to increase as well.

Okay… But why does it work?

I didn’t expect to have such a hard time grasping this. On some level it just feels weird to ‘arbitrarily’ alter the distribution of every affine layer’s output just because it’s convenient for us. It feels even weirder that it also improves model accuracy, and doesn’t simply reduce the rate of model failure.

I assumed that since this method is noted as a breakthrough discovery and has such a large impact on the ease of training & efficacy of models that it must have some well-defined theoretical basis to explain itself. Turning again to Ioffe & Szegedy, they assert that it “reduces internal covariate shift”, but I struggled to follow their reasoning. Apparently, this may not have been my own fault, as Santurkar et al. argue against internal covariate shift and submit a mathematical proof for their own hypothesis - that batchnorm actually smooths the optimization landscape, increasing the stability and predictive capability of gradients in the space.

I can’t admit to understanding their proof, but I found their deconstruction of internal covariate shift quite persuasive, and the fact that this paper directly addresses the ‘why accuracy increases’ question helped reassure my poor brain.

I’ve implemented batchnorm per the coursework’s instructions and verified it’s correct using the given unit tests. I have the forward pass logic calling correctly inside the net, but not backward pass yet. Once I get that in place, the assignment is complete.

Also note layer normalization is a variant of batch norm. It’s become quite popular since its inception - overtaking batch norm for paper citations:

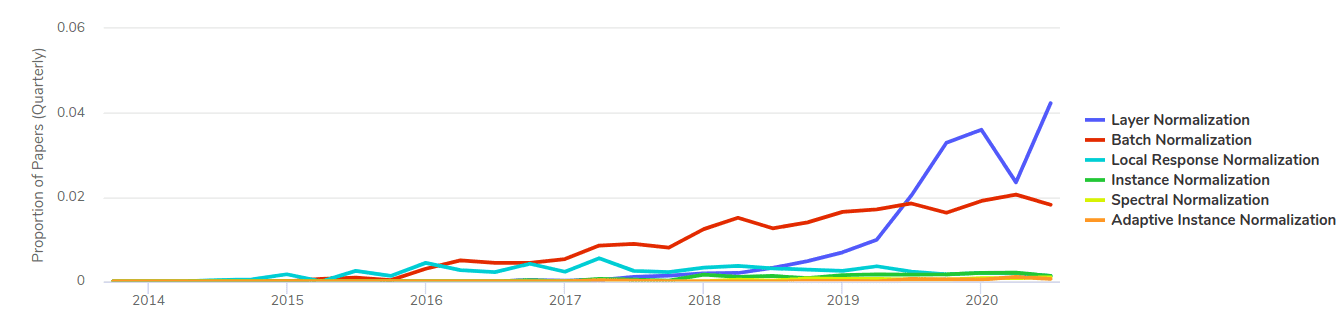
Image Source: https://paperswithcode.com/method/layer-normalization

I found https://theaisummer.com/normalization/ to be a useful resource in understanding the relationship between batch & layer norms.