Archive: Softmax classifier

Published: 2021-04-01
Updated: 2023-09-01

Note: Originally posted April 1st, 2021, this is post $2$ in the archived Deep Learning for Computer Vision series (cs231n).

Browse the full cs231n series.
See the source code in the softmax notebook.

New comments are found exclusively in info boxes like this one.

The third part of A1 has students write a linear softmax classifier. cs231n has softmax notes, but I found this article to be generally more approachable and more in-depth.

The term Softmax loss is a little weird in that softmax loss isn’t really meaningful in and of itself - it’s actually cross-entropy loss applied to softmax output. The output of the Softmax function can be interpreted probabilistically, so in applying the cross-entropy function to Softmax’s output, we get either a MLE or MAP estimation of the underlying distribution (MLE if no regularization, MAP if so). I’m not versed in either probability or information theory enough to get any more detailed than that (hand-wavey) description though.

As given by the cs231n notes, the loss $L$ at sample $i$ is:

L_i = -log{\left( \frac {e^{f_{y_i}}} {\sum_j e^{f_j}} \right)}

Note: At the time, I didn’t do a great job here defining my terms, so let’s make up for that now:

f_{y_i}

denotes your model's score at the ground-truth label's index.

e^{f_{y_i}}

is just that score, exponentiated.

\sum_j e^{f_j}

denotes the exponentiated sum of all

j \in K

classes (10, for CIFAR-10) at sample

i

. That naturally includes the target index, i.e. where

j=y_i

It’s shorthand, and a slight abuse of notation. The kind which you grow to get used to (eventually).

We need an applicable gradient, but this time the cs231n notes aren’t giving me one. While the notes and sources below each use different notation, you can find gradient derivations on two of the pages mentioned before (1, 2). The important insight is:

… the gradient of the cross-entropy loss for logistic regression is the same as the gradient of the squared error loss for Linear regression.

Hence they each simplify down to familiar-ish results. From to Eli’s Blog:

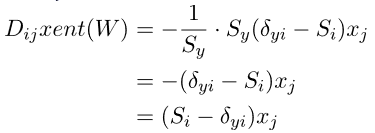
Where $S_i$ denotes the Softmax vector, and

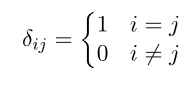
Once you implement this in code, the rest of the exercise is effectively identical to the SVM one, so I won’t repeat myself covering the steps to complete it.

Note: That implementation can be found in softmax.py.

Results

On the validation set, I get accuracy of 34.4%, which is consistent with the assignment’s assertion that if you look for more optimal hyperparameters you can achieve validation accuracy just above 35%.

This is comparable to (though marginally worse than) the SVM classifier, which yielded validation accuracy of 36.5% using the same hyperparameters.